Riceviamo da Carlo Doglioni questo commento, che pubblichiamo come contributo indipendente, all’intervista a Gianluca Valensise
https://terremotiegrandirischi.com/2019/12/17/gravimoti-un-nuovo-paradigma-intervista-a-gianluca-valensise/
 
Carlo Doglioni, geologo, è professore di geodinamica all’Università Sapienza di Roma dal 1997. Dal 2009 al 2014 è stato presidente della Società Geologica Italiana; dal 2009 è membro dell’Accademia dei Lincei e dal 2011 dell’Accademia dei XL. Dal 27 aprile 2016 è presidente dell’Istituto Nazionale di Geofisica e Vulcanologia.

La teoria del rimbalzo elastico è stata una grande innovazione all’inizio del secolo scorso. Questo modello assumeva l’ipotesi che le faglie sismogenetiche fossero “prevedibili” nel loro comportamento e che tendessero alla rottura in modo simile e con la stessa magnitudo in un ciclo potenzialmente infinito. Questa assunzione, indistinta per gli ambienti tettonici estensionali, compressivi o trascorrenti, si è dimostrata poco attinente alla realtà più complessa del ciclo sismico.
I terremoti estensionali hanno per esempio un certo numero di differenze rispetto a quelli compressivi che non possono essere spiegate se non con meccanismi genetici diversi.

Sono stato revisore dell’articolo di Segall & Heimisson (BSSA, 2019) e quindi parlo con conoscenza di causa. Gli autori travisano il comportamento elastico della crosta superiore con l’energia elastica accumulata nell’intersismico negli ambienti estensionali, che non c’è, quantomeno quella necessaria al rimbalzo elastico.

Uno dei principali osservabili “accantonato” nella teoria del rimbalzo elastico, considerato invece nel modello dei gravimoti, è la distribuzione dello stress con la profondità. Notoriamente, negli ambienti estensionali, lo stress massimo è all’incirca verticale e parallelo al carico litostatico. Quello che nel modello del rimbalzo elastico, e di conseguenza anche nell’articolo di Segall & Heimisson non funziona clamorosamente è l’assumere che la crosta sia soggetta ad un tiro estensionale: ciò è falso perché sotto 1 km circa di profondità, la crosta è in compressione anche negli ambienti estensionali perché il carico litostatico si ripartisce nel volume e va ad annullare ed invertire la componente orizzontale negativa (estensione) dello stress minimo, che diventa positivo e quindi necessariamente compressivo.

Questa condizione, nota anche nei libri di testo, previene ogni possibilità di avere un tiro orizzontale (con stress minimo, cioè il sigma 3, negativo) che possa generare un rimbalzo elastico. Il carico litostatico aumenta di circa 25-27 MPa/km e sotto 1 km anche il sigma minimo diventa positivo, cioè compressivo: si legga per esempio Twiss & Moores, “Structural Geology” pag 190-191:

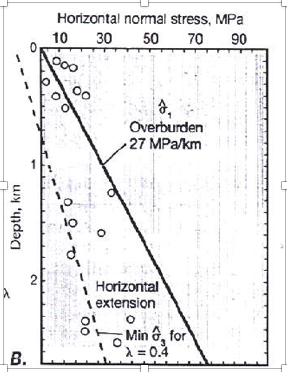
Note that the plot of minimum values of sigma3 in Figure 10.5A indicates that actual tensile stresses (negative values of the normal stress) cannot exist below a depth of about 1 km. In fact, tensile stresses have not been measured within the Earth at all.

Figure 10.5A Il sigma minimo (3) sotto 1 km è sempre positivo (compressivo), anche negli ambienti estensionali.

Fig. 9.20 Orientation of the most critically stressed Griffith crack under applied confined compression. The crack is closed, and the orientation of the most criticallynstressed crack falls in the range 45°<b°<90°. A local tensile stress concentration develops near, but not at, the crack tips and is maximum at an angle d°>0°. The local tensile stress maximum sigma1 is oriented such that the crack grows progressively toward parallelism with d1. Crack growth must be accommodated by frictional sliding on the closed part of the crack surface. 

Nel modello dei gravimoti, la crosta superiore ha una reologia sostanzialmente elastica, ma questo non è il punto: il modello di Okada, per esempio, non è messo in discussione dai gravimoti, perché si riferisce alla deformazione modellabile una volta assunto un piano di una certa dimensione e con un determinato slip in un mezzo elastico. Tutto ciò rimane valido e verificato. Il punto nodale è la forza che ha generato il movimento: l’energia sprigionata dai terremoti è accumulata nei volumi e le faglie rilasciano la componente elastica che viene dissipata durante lo slip.
Un’altra mistificazione dei gravimoti è che non generino la doppia coppia: questa è garantita dallo scivolamento lungo il piano di faglia normale e quindi lo shear relativo è rappresentabile come una doppia coppia. Non è dunque un argomento che possa mettere in discussione il modello dei gravimoti. La doppia coppia non ha nulla a che vedere con i volumi ma è un sistema di rappresentazione delle forze, che non è in contrasto con lo scivolamento del tetto della faglia dovuto alla gravità e non a un tiro orizzontale.

Le differenze tra gli ambienti tettonici compressivi ed estensionali sono numerose:

• Il b-value della Gutenberg-Richter a scala globale è 1.1 per le faglie normali, mentre è 0.9 per i sovrascorrimenti (Schorlemmer et al., 2005): infatti i terremoti estensionali hanno magnitudo anche di due gradi inferiori.
• La magnitudo massima, di conseguenza è minore per i terremoti estensionali (raramente supera i 7.5) rispetto ai terremoti compressivi che sappiamo arrivare almeno a M 9.5.
• Nella crosta, i volumi coinvolti dalla tettonica estensionale e di conseguenza la lunghezza delle faglie per i terremoti estensionali hanno una lunghezza che è circa 3 volte lo spessore sismogenetico per gli ambienti estensionali, mentre può superare le 25 volte in quelli compressivi.
• Gli aftershock durano molto di più per le faglie normali e quindi la legge di Omori ha un esponente diverso per la durata delle sequenze estensionali. Questo è coerente col fatto che i volumi si muovono in favore di gravità negli ambienti distensivi e continuano a muoversi finché non raggiungono il proprio equilibrio gravitazionale, esattamente il contrario degli ambienti compressivi in cui i volumi devono muoversi contro la gravità.
• Un’altra asimmetria tra terremoti estensionali e compressivi, a parità di magnitudo, è lo stress drop che è maggiore per i terremoti compressivi rispetto a quelli estensionali (si veda Cocco & Rovelli, 1989, JGR).
• Gli eventi compressivi si enucleano preferibilmente in aree a basso sigma3 (carico litostatico), mentre gli eventi estensionali aumentano di magnitudo con la crescita del sigma1 (carico litostatico), oltre ad avere una migrazione della rottura spesso opposta; si veda Carminati et al. (2004).
• Il comportamento dei fluidi nel cosismico è opposto tra i due sistemi tettonici (Doglioni et al., 2014); i fluidi sono contenuti nelle fratture e la loro espulsione necessita la chiusura di queste discontinuità formatesi precedentemente nell’intersismico. A questo proposito l’aumento del rapporto Vp/Vs conforta questa interpretazione (Lucente et al. 2010). Pre-, ma soprattutto rialzi cosismici delle falde, aumento della portata delle sorgenti, dei contenuti salini e delle temperature sono stati ampiamente documentati e questi rilasci di fluidi necessitano il restringimento della porosità di frattura preesistente (Barberio et al., 2017; Petitta et al., 2018, ecc.).

Negli articoli sui gravimoti (https://www.nature.com/articles/srep12110), al di là della terminologia e classificazione per identificare fenomeni diversi della natura, così come avviene per la tassonomia delle piante, l’energia rilasciata dal collasso gravitazionale è enormemente superiore a quella liberata dalle onde sismiche: questo ha un doppio significato, cioè 1) l’energia gravitazionale è di gran lunga maggiore rispetto a quella rilasciata dalle onde sismiche ed è quindi più che sufficiente per mobilizzare i volumi a tetto delle faglie normali e generare terremoti estensionali e 2) l’energia in eccesso spiega la deformazione tramite piegamento e fratturazione del volume a tetto (e in parte anche a letto) dei piani di faglia, e il calore di frizione.

Veniamo ai volumi dilatati nell’intersismico negli ambienti estensionali che sono previsti da tutte le modellazioni numeriche al di sopra della transizione fragile-duttile (per esempio Doglioni et al., PEPI 2011). Il rimbalzo elastico necessita di un rimbalzo cosismico prevalente orizzontale, mentre in realtà il movimento dominante è verticale. In un ambiente estensionale il volume comprime verso il basso e può ‘richiudere’ almeno parzialmente il cuneo pre-dilatato durante l’intersismico.

Le rocce fratturate hanno un coefficiente di Poisson minore rispetto a quelle non fratturate. Inoltre il coefficiente di Poisson dipende dalla temperatura e dalla pressione che aumentano con la profondità. Proprio per le proprietà meccaniche, le rocce sovracompresse possono accumulare molta più energia elastica di quanto ne possano accumulare in trazione. Le rocce si fratturano in estensione con un’energia almeno 10 volte inferiore a quella necessaria in contrazione. Anche questo implica una profonda differenza di comportamento meccanico tra le due condizioni tettoniche e di resistenza alla deformazione. Le rocce, una volta fratturate perdono gran parte della loro elasticità. Il paradosso che non esiste trazione negli ambienti estensionali perché tutti e tre i tensori di sforzo sono compressivi è superato dallo stress deviatorico, che agisce in maniera differenziale tra il livello fragile e quello duttile, avendo strain-rate diversi per la loro reologia opposta. Quindi il volume extra che subisce la subsidenza cosismica è naturalmente maggiore negli ambienti estensionali perché va a riprendersi il volume dilatatosi nell’intersismico, ma ciò vale all’opposto anche per gli ambienti compressivi che nel cosismico dilatano invece il volume sovracompresso nell’intersismico a tetto della rampa del sovrascorrimento e che sfogano l’energia, muovendo un volume maggiore verso l’alto (in atmosfera o in mare), senza confinamento, piuttosto che nel sottosuolo.

Segall & Heimisson travisano il contenuto dell’articolo di Bignami et al. 2019 ignorando le basi della geodinamica. Il loro modello assume, come già in Okada, un semispazio elastico infinito isotropico, senza considerare la transizione fragile duttile alla base, condizioni abbastanza irrealistiche. Il modello di Segall & Heimisson non spiega inoltre dove vada a finire il volume mancante in sollevamento. Il loro articolo dice che il volume mancante è un artificio della finitezza del dominio di integrazione, senza escludere che i volumi siano differenti e che per dirimere la questione sia necessario trattare in maniera più approfondita gli errori di misura e di metodo. Inoltre confermano la geometria superficiale in funzione della dislocazione, come già dimostrato da Okada.

Bignami et al. (2019), ma anche Valerio et al. (2018), dimostrano invece che con una tecnica oramai consolidata e di grande risoluzione in termini di minimizzazione dell’errore, c’è uno sbilanciamento di volumi oltre 7 volte maggiore per il volume abbassatosi, che è plausibile solo se vi è un volume pre-dilatato in profondità in grado di assorbire questa grande differenza di massa non riconciliabile con ritiri elastici istantanei. Bignami et al. dimostrano che la deformazione gravitazionale di un mezzo elastico non corrisponde necessariamente a una sorgente energetica di energia elastica.

Segall & Heimisson utilizzano una sorgente puntiforme certamente non in grado di raggiungere la raffinatezza che viene ottenuta oramai dai dati SAR. E’ utile ricordare che l’utilizzo del rimbalzo elastico, che loro invocano, e di ciò che ne consegue (terremoto caratteristico e relativi tempi di ritorno) hanno portato in passato a numerosi errori di valutazione.

Che i graviquakes siano ancora poco accettati è certamente vero, ma ciò non significa che siano sbagliati e rimane il fatto che almeno una decina di riviste internazionali e loro revisori ne hanno ‘promosso’ le evidenze e la modellazione. Qualcuno inoltre inizia a considerare la sismicità estensionale come legata principalmente alla gravità: si veda per esempio Thomson & Parson (2017, PNAS).

In questo breve commento ho omesso per brevità gli ambienti trascorrenti che sono controllati dall’elasticità del mezzo e del rapporto tra la frizione statica del volume crostale con la frizione statica sui piani di faglia, piani che possono essere molto numerosi (si veda la recente sequenza di Ridgecrest 2019, dove sono state mappate oltre 200 faglie attivatesi durante i due mainshock). Solo quando la tettonica trascorrente diventa transtensiva, la componente elastica deve sommarsi alla componente gravitazionale, diminuendo mano a mano che da transtensione si passa a estensione pura.

Vale la pena aggiungere alcuni chiarimenti sulla metodologia utilizzata, a riprova della inesatta analisi dei dati riportati nel citato Bignami et al. 2019, sia da parte di Segall & Heimisson che dal commento di Valensise, e del fatto che il metodo è del tutto corretto. Se si osserva la mappa dei punti che ricadono nell’intervallo -3cm/+3cm (figura in basso) si evince che tale intervallo di deformazioni è praticamente distribuito su tutta la mappa, ad esclusione delle are in subsidenza e sollevamento causate dal terremoto del 2016:

L’analisi statistica di questi dati ci dice che questi punti (sono 663533) con deformazione compresa tra -3 e +3 cm hanno valor medio pari a 0.4437 cm, il che significa che l’immagine, globalmente, ha un bias verso l’alto di circa 4.4 mm che, in quanto tale, non incide sulla differenza tra volumi in sollevamento e volumi in subsidenza.

Se sommiamo le deformazioni dei punti (algebricamente e con bias incluso) si ottiene uno spostamento totale di superficie (ERRATO perché c’è un bias) pari a: 0.00258 km3 (ancora al di sotto del 20% di sottostima). Ma questo conto è errato, proprio per il bias sopracitato, altrimenti dovremmo pensare che si è sollevata mezza Italia tutta insieme. Rimuovendo in modo del tutto corretto il bias, che è indifferente rispetto al calcolo volume up/down relativo, si ottiene un numero ben diverso: -1.02222E-06 km3.
Questo conferma che le misure SAR sono assolutamente affidabili e accurate, molto più di un estremante semplice modello puntiforme proposto da Segall & Heimisson.

L’articolo di Valensise contiene anche altre inesattezze relativamente alla presunta deformazione verso l’Adriatico, dedotte da fonti che presumiamo siano diverse dall’articolo di Bignami et al. 2019. I dati di quest’ultimo mostrano che la deformazione si assesta intorno allo zero man mano che ci si allontana dall’epicentro verso est:

Zoomando nella parte più a est si nota che la deformazione è entro la fascia -3/+ 3 cm di tolleranza, con tendenza anche in abbassamento:

D’altra parte la citata figura 5 tratta da Bignami et al., è ben lontana dalla zona costiera, e non dà informazioni rispetto a cosa succede allontanandosi dell’area epicentrale.

Si fa notare che il SAR non è “cieco” in quel range -3/+3 cm, che è semplicemente la fascia di incertezza per questa specifica mappa fatta con questi specifici dati, un rumore sulla misura che non ci consente di discriminare tra deformazione certamente positiva e certamente negativa, motivo per cui sono state utilizzate tali soglie. Infine, a riprova della scarsa attenzione prestata nella lettura, i dati usati da Bignami et al. 2019, non sono dei satelliti Sentinel dell’Agenzia Spaziale Europea (ESA), bensì del satellite ALOS2, dell’Agenzia Spaziale Giapponese.

Per concludere chiediamoci: negli ambienti estensionali la forza accumulata è dunque l’energia elastica di trazione che non esiste, o è invece la componente gravitazionale che è certa? Questa seconda naturale interpretazione non inficia lo slip in un mezzo elastico. Anche una molla che cade rilascia energia gravitazionale.

Il rasoio di Occam è un percorso mentale utilissimo, ma non può essere un alibi per omettere i dati di fatto. Anzi, Il rasoio di Occam è a favore della energia gravitazionale che sicuramente esiste, in quanto non richiede l’esistenza della trazione elastica che sarebbe una forza aggiuntiva per gli ambienti estensionali.

Carlo Doglioni

Barberio, M.D., Barbieri, M., Billi, A., Doglioni, C., Petitta, M., 2017. Hydrogeochemical changes before and during the 2016 Amatrice-Norcia seismic sequence (central Italy). Scientific Reports, 7, 11735, doi:10.1038/s41598-017-11990-8, https://www.nature.com/articles/s41598-017-11990-8

Barberio M.D., Gori F., Barbieri M., Billi A., Devoti R., Doglioni C., Petitta M., Riguzzi F., Rusi S. 2018. Diurnal and semidiurnal cyclicity of Radon (222Rn) in groundwater, Giardino Spring, central Apennines, Italy. Water, 10, 1276; doi:10.3390/w10091276. https://www.mdpi.com/2073-4441/10/9/1276

Bignami C., Valerio E., Carminati E., Doglioni C., Tizzani P. 2019. Volume unbalance on the 2016 Amatrice – Norcia (central Italy) seismic sequence and insights on normal fault earthquake mechanism. Scientific Reports, 9:4250 | https://doi.org/10.1038/s41598-019-40958-z

Carminati E., Bignami C., Doglioni C., Smeraglia L., 2020. Lithological control on multiple surface ruptures during the 2016-2017 Amatrice-Norcia seismic sequence. Journal of Geodynamics, in press. doi.org/10.1016/j.jog.2019.101676

Carminati E., Doglioni C. & Barba S. (2004): Reverse migration of seismicity on thrusts and normal faults. Earth Science Reviews, 65, 195–222.

Cocco M. & Rovelli A., 1989. Evidence for the Variation of Stress Drop Between Normal and Thrust Faulting Earthquake in Italy. J. Geophys. Res. 94, B7, 9399-9416.

Doglioni C., Barba S., Carminati E. Riguzzi F., 2015. Fault on-off versus strain rate and earthquakes energy. Geoscience Frontiers 6, 265-276, doi: http://dx.doi.org/10.1016/j.gsf.2013.12.007

Doglioni C., Barba S., Carminati E. Riguzzi F., 2014. Fault on-off versus coseismic fluids reaction. Geoscience Frontiers, v. 5, issue 6, pp. 767–780, doi.org/10.1016/j.gsf.2013.08.004

Doglioni C., Carminati E., Petricca P., Riguzzi F. 2015 Normal fault earthquakes or graviquakes. Scientific Reports, 5, 12110 doi:10.1038/srep12110. https://www.nature.com/articles/srep12110

Doglioni, C., Barba, S., Carminati, E. & Riguzzi, F. 2011. Role of the brittle-ductile transition on fault activation. Phys. Earth Planet. Int., 184, 160–171, https://www.sciencedirect.com/science/article/pii/S0031920110002384

Liberatore, D., Doglioni, C., Al Shawa, O., Atzori, S., Sorrentino, L. 2018. Effects of coseismic ground vertical motion on masonry constructions damage during the 2016 Amatrice-Norcia (Central Italy) earthquakes. Soil Dynamics and Earthquake Engineering, 120 (2019) 423–435, https://doi.org/10.1016/j.soildyn.2019.02.015

Lucente, F.P., De Gori, P., Margheriti, L., Piccinini, D., Di Bona, M., Chiarabba, C., Piana Agostinetti, N., 2010. Temporal variation of seismic velocity and anisotropy before the 2009 Mw 6.3 L’Aquila earthquake, Italy. Geology 38 (11), 1015e1018. http://dx.doi.org/10.1130/G31463.1.

Moro, M., Saroli, M., Stramondo, S., Bignami, C., Albano, M., Falcucci, E., Gori, S., Doglioni, C., Polcari, M., Tallini, M., Macerola, L., Novali, F., Costantini, M., Malvarosa, F. and Wegmüller, U., 2017. New insights into earthquake precursors from InSAR. Scientific Reports, 7, 12035, doi:10.1038/s41598-017-12058-3, https://www.nature.com/articles/s41598-017-12058-3

Petitta M., Mastrorillo L., Preziosi E., Banzato F., Barberio M.D., Billi A., Cambi C., De Luca G., Di Carlo P., Di Curzio D., Di Salvo C., Nanni T., Palpacelli S., Rusi S., Saroli M., Tallini M., Tazioli A., Valigi D., Vivalda P., Doglioni C., 2018. Water table and discharge changes associated with the 2016-2017 seismic sequence in central Italy: hydrogeological data and conceptual model for fractured carbonate aquifers. Hydrogeology Journal, https://doi.org/10.1007/s10040-017-1717-7

Petricca P., Barba S., Carminati E., Doglioni C., Riguzzi F. 2015. Graviquakes in Italy. Tectonophysics, 656, 202–214, doi:10.1016/j.tecto.2015.07.001

Petricca, P., Carminati, E., Doglioni, C. and Riguzzi, F., 2018. Brittle-ductile transition depth versus convergence rate: impact on seismicity. Physics of the Earth and Planetary Interior, doi.org/10.1016/j.pepi.2018.09.002

Petricca P., Carminati E. and Doglioni C., 2019. The Decollement Depth of Active Thrust Faults in Italy: Implications on Potential Earthquake Magnitude. Tectonics, 38. https://doi.org/10.1029/ 2019TC005641

Plastino W., Panza G.F., Doglioni C., Frezzotti M.L., Peccerillo A., De Felice P., Bella F., Povinec P.P., Nisi S., Ioannucci L., Aprili P., Balata M., Cozzella M.L., Laubenstein M., 2011. Uranium groundwater anomalies and active normal faulting. J Radioanal Nucl Chem, 288, 101–107.

Riguzzi, F. Crespi, M., Devoti, R., Doglioni, C. Pietrantonio, G. and Pisani, A.R., 2012. Geodetic strain rate and earthquake size: New clues for seismic hazard studies. Physics of the Earth and Planetary Interiors 206-207, 67–75, https://www.sciencedirect.com/science/article/pii/S0031920112001264

Riguzzi F., Crespi M., Devoti R., Doglioni C., Pietrantonio G., Pisani A.R., 2013. Strain rate relaxation of normal and thrust faults in Italy. Geophysical Journal International. doi: 10.1093/gji/ggt304

Schorlemmer, D., Wiemer, S. & Wyss, M. 2005. Variations in earthquake-size distribution across different stress regimes. Nature 437, 22.

Segall P. & Heimisson E.R., 2019. On the Integrated Surface Uplift for Dip‐Slip Faults. Bulletin of the Seismological Society of America (2019) 109 (6): 2738-2740.
https://doi.org/10.1785/0120190220

Smeraglia L., Bernasconi S.M., Berra F., Billi A., Boschi C., Caracausi A., Carminati E., Castorina F., Doglioni C., Italiano F., Rizzo A.L., Uysal T., Zhao X-J. 2018. Crustal-scale fluid circulation and co-seismic shallow comb-veining along the longest normal fault of the central Apennines, Italy. Earth Planet. Sci. Lett., 498, 152-168, https://doi.org/10.1016/j.epsl.2018.06.013.

Thompson, G. A. & Parsons, T. 2017. From coseismic offsets to fault-block mountains. PNAS 114, 9820–9825, https://doi.org/10.1073/pnas.1711203114 (2017).

Valerio, E. Tizzani, P., Carminati, E., Doglioni C., 2017. Longer aftershocks duration in extensional tectonic settings. Scientific Reports, 7, 16403 doi:10.1038/s41598-017-14550-2, https://www.nature.com/articles/s41598-017-14550-2

Valerio, E., Tizzani, P., Carminati, E., Doglioni, C., Pepe, S., Petricca, P., De Luca, C., Bignami, C., Solaro, G., Castaldo, R., De Novellis, V. and Lanari, R. 2018. Ground Deformation and Source Geometry of the 30 October 2016 Mw 6.5 Norcia Earthquake (Central Italy) Investigated Through Seismological Data, DInSAR Measurements, and Numerical Modelling. Remote Sensing, 10, 1901, doi:10.3390/rs10121901, https://www.mdpi.com/2072-4292/10/12/1901